ONLINE MOORING CALCULATORS
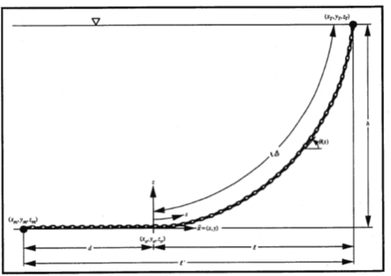
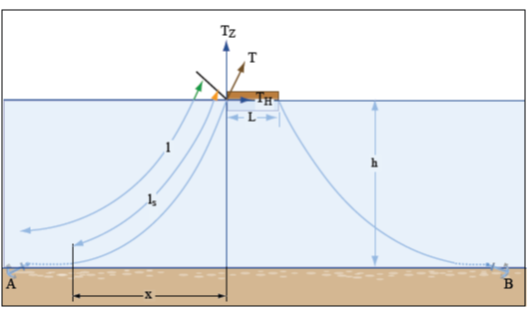
- MOORING LINE CATENARY CALCULATION
- RADIUS OF GYRATION CALCULATION FOR SHIP LOADING CONDITION
- PIER SIDE SHIP BERTHING LOAD CALCULATION
- MOORING BRIDLE PLATE OR PADEYE DESIGN VERIFICATION
- MOORING WINCH BRAKE AND PULL CAPACITY ON DIFFERENT LAYERS
- MOORING BERTHING AND ANCHORAGE ENVIRONMENTAL LOADS ON TANKERS AND GAS CARRIERS (OCIMF-SIGTTO)
- API WIND AND CURRENT LOAD CALCULATION
- SHIPMOOR-WHARF OR PIERSIDE MOORING ANALYSIS SOFTWARE
MOORING DESIGN & MOORING ANALYSIS OF BARGE
This article presents the methodology of mooring analysis for accommodation barge,crane barge, offshore support barges in a given water depth.
MOORING ARRANGEMENT OF BARGE
Barge is connected to sea floor by catenary lines. These catenary lines exert force on the barge so that it can remain close to target position. Due to environmental forces on the floating body, it will try to move from its initial location. So mooring lines will try to restrain floating body and there will be a equilibrium in environmental forces and catenary line forces.
|
|
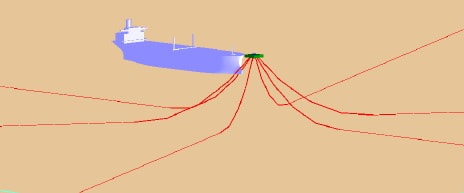
Mooring Arrangement of Offshore Support Barge
|
Offshore Support barges are moored in proximity of offshore jackets or platforms. There main objective are to provide logistic ,cargo and manpower support to platform. Based on the size of barge, they have 4 or 8 point mooring system. While designing of mooring arrangement of these barges, clearance from platform shall be determined and any tangling of mooring lines with jacket legs shall be avoided. |
|
Mooring Arrangement of Offshore Heavy Lifting Barge
|
Normally heavy lift is performed by this kind of lifting barges. They normally have 8 or 12 point mooring system. During lifting of jacket, platform or other offshore structure, 1 st order surge and sway oscillations are kept at minimum so that operability of installation of offshore structures can be increased. |
|
Mooring Arrangement of Offshore Pipelay Barge
|
Pipe laying barges move on the set track of pipe laying and barge moves with certain speed. So continuous engagement of mooring winches are required so that barge can maintain its direction. |
|
Mooring Arrangement of FPSO |
Turret mooring of FPSO
|
MOORING ANALYSIS OF BARGE
Purpose of Mooring Analysis
A floating ship/barge held on location with mooring system, When wind, current and waves act on the vessel, the total environmental force (F) pushes the vessel a distance (x) away from its initial position over the hole. The vessel comes to an equilibrium position when the mooring develops a net restoring force equal to the steady-state environmental force.
Wind, waves, and current induce movement of the vessel away from the target location and increase the tension in the windward mooring lines while decreasing tension in the leeward lines. Each mooring should be analyzed to ensure that developed tension (Tmax) does not exceed the maximum safe working load and that the load placed on the anchor (Amax) does not exceed its holding power. The holding power of an anchor is significantly reduced when the anchor is subjected to a vertical load. To completely avoid vertical loads, the length of mooring line outboard of the fairlead must be long enough to allow the line to remain tangent to the sea bottom at the anchor during periods of the highest expected line tensions. Also, the vessel movements should be kept within certain limits that can be tolerated by the drilling riser.
A mooring analysis is often performed in conjunction with a riser analysis to determine:
A floating ship/barge held on location with mooring system, When wind, current and waves act on the vessel, the total environmental force (F) pushes the vessel a distance (x) away from its initial position over the hole. The vessel comes to an equilibrium position when the mooring develops a net restoring force equal to the steady-state environmental force.
Wind, waves, and current induce movement of the vessel away from the target location and increase the tension in the windward mooring lines while decreasing tension in the leeward lines. Each mooring should be analyzed to ensure that developed tension (Tmax) does not exceed the maximum safe working load and that the load placed on the anchor (Amax) does not exceed its holding power. The holding power of an anchor is significantly reduced when the anchor is subjected to a vertical load. To completely avoid vertical loads, the length of mooring line outboard of the fairlead must be long enough to allow the line to remain tangent to the sea bottom at the anchor during periods of the highest expected line tensions. Also, the vessel movements should be kept within certain limits that can be tolerated by the drilling riser.
A mooring analysis is often performed in conjunction with a riser analysis to determine:
- Limiting environments for operating and survival conditions
- Recommended mooring pattern
- Required length of mooring line outboard of the fairlead
- Initial line tension
- Test load requirements for anchor
- Piggyback anchor requirements
- Operational concerns such as the need for slackening the leeward lines during a storm
- Special details such as the clearance between a mooring line and a nearby pipeline
Hydrodynamics modelling for Mooring Analysis
External Forces on Moored Barge
- Static forces (current, wind, and a mean wave force),
- Direct wave forces (forces at the wave period), and
- Non wave period forces (wave drift and wind gusts)
Barge Loading Condition
Barge loading condition in moored condition shall be defined approximately and any variation in consumables, deck load etc shall be considered for worst load case scenario.
Inertia Calculation of Barge for Mooring Analysis
Moments of inertia are assessed using the estimated gyration radii of the vessel,
Roll inertia radius,
Pitch and Yaw inertia radii,
weight, m = displacement
Roll inertia radius,
Pitch and Yaw inertia radii,
weight, m = displacement
|
The calculation of roll motion is a key point of any ship motion calculations. It is governed by the roll damping, which is caused by two main contributions:
Cd is quadratic damping coefficient (equal to 0.05 for this barge without a bilge keel), ρ is sea water density (equal to 1025 kg/m3), B is the breadth of the vessel, L is the length of the vessel. |
Hydrodynamic mesh for barge Mooring Analysis
|
Additional Linear Damping for Low Frequency Motions for Mooring Analysis
Additional linear damping shall be calculated for spread moored vessel:
It should be noted that Maxx, Mayy, Maψψ are the diagonal terms of the asymptotic added mass matrix of the vessel. And Koxx, Koyy, Koψψ are the diagonal terms of the mooring stiffness matrix [Ko] evaluated at the average position of the vessel.
It should be noted that Maxx, Mayy, Maψψ are the diagonal terms of the asymptotic added mass matrix of the vessel. And Koxx, Koyy, Koψψ are the diagonal terms of the mooring stiffness matrix [Ko] evaluated at the average position of the vessel.
Wind and Current Loads in Mooring Analysis
Wind Load Calculation for Mooring Analysis
Wind loads can be calculated with wind tunnel test, API RP 2SK guidelines etc.Projected area and wind force application point are required for wind force determination.
The steady state force (for bow or beam environment) due to wind acting on a moored floating unit can be determined using following Equation,
Fw = Cw × Σ (Cs×Ch×A) ×Vw²
Where:
Fw = wind force, lbs (N),
Cw = 0.0034 lb/(ft² • kt²) (0.615 N• sec²/m4)
Cs = shape coefficient,
Ch = height coefficient,
A = vertical projected area of each surface exposed to the wind, ft² (m²),
Vw = design and speed, knots (m/sec).
Wind shielding in accordance with acceptable methods shall be considered as per API RP 2SK guidelines. For API method,The equations presented are convenient for calculating wind and current forces for bow and beam environments.
The steady state force (for bow or beam environment) due to wind acting on a moored floating unit can be determined using following Equation,
Fw = Cw × Σ (Cs×Ch×A) ×Vw²
Where:
Fw = wind force, lbs (N),
Cw = 0.0034 lb/(ft² • kt²) (0.615 N• sec²/m4)
Cs = shape coefficient,
Ch = height coefficient,
A = vertical projected area of each surface exposed to the wind, ft² (m²),
Vw = design and speed, knots (m/sec).
Wind shielding in accordance with acceptable methods shall be considered as per API RP 2SK guidelines. For API method,The equations presented are convenient for calculating wind and current forces for bow and beam environments.
Current Load for Mooring Analysis
Current Load Calculation for Mooring Analysis
Fcx = Ccx×Σ S×Vc²
Fcy = Ccy×Σ S×Vc²
Where:
Fcx = current force on the bow (N)
Fcy = current force on the beam (N)
Ccx = ½ * ρWater * Shape Coefficient (considered 1) = 502.7 Nsec²/m4
Ccy = ½ * ρWater * Shape Coefficient (considered 1) = 502.7 Nsec²/m4
S = wetted surface area of the hull (m²)
Vc = design current speed (m/sec)
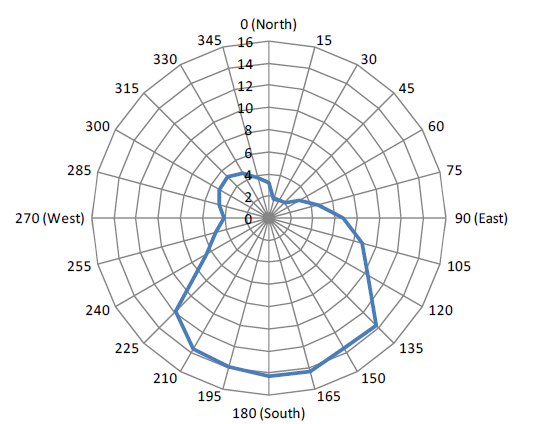
The graph below shows the value of coefficient multiplied with surface area at different angle of incidences.
API Current load calculator
Fcy = Ccy×Σ S×Vc²
Where:
Fcx = current force on the bow (N)
Fcy = current force on the beam (N)
Ccx = ½ * ρWater * Shape Coefficient (considered 1) = 502.7 Nsec²/m4
Ccy = ½ * ρWater * Shape Coefficient (considered 1) = 502.7 Nsec²/m4
S = wetted surface area of the hull (m²)
Vc = design current speed (m/sec)
The graph below shows the value of coefficient multiplied with surface area at different angle of incidences.
API Current load calculator
Mooring Lines Properties
|
The main characteristics of the mooring wire ropes like Number of Lines, Length on Each Drum,Diameter,Weight in Air, Weight Submerged, Axial Stiffness and MBL etc shall be defined.
Anchor DataAnchor arrangement and holding capacity in soft or hard clay shall be defined.
Mooring WinchesMooring winch location, pull capacity on different layers, MBL etc shall be defined.
|
Mooring Pattern of barge
|
Wave Model
Wave is modeled with JONSWAP spectrum using significant wave height Hs, the peak period Tp, and the shape parameter Gamma.
Operating waves
For the operating position significant wave height range of that particular month or period shall be used. Each Hs shall be allocated three Tp based on the Noble Denton guidelines. Gamma can be used as 3.3.
Extreme waves
Based on the operational periods, the monthly extreme value at field location shall be used which can be extracted from metocean report. The Tp used for standoff position shall be taken with margin i.e as +/- 30% of the associated Tp of monthly extreme value.
Analysis Methodology
Capabilities of the mooring system shall be computed using quasi-dynamic simulations of the vessel and the mooring system under combination of wind, wave and current environmental loads. Simulations shall consider combining wave frequency and low frequency responses of the system to get the maximum vessel motions and mooring line tensions.
Simulations shall performed for 3 hours duration environments. “Quasi-dynamic analysis” is performed, meaning that full dynamic motion of the vessel is considered but line tensions are estimated from vessel dynamic motions with static restoring curves.
The low frequency motion shall be computed in time domain while the wave frequency motion shall be calculated in frequency domain. The global dynamic motion is the superposition of the low frequency motion and the wave frequency motion, the stiffness shall be computed for the sum of the WF and LF motion.
The tension in the mooring line shall be higher than horizontal component. For mooring chain laying on the ground, there will be a constant difference in line tension and horizontal component of restoring force. Once the mooring chain gets up from bottom, these two force becomes almost same.
If mooring line stiffness is small, small change in force will produce large changes in position. For this reason, if one wants to stay close to a given position, he makes lines work in pairs. Suppose that we have two of the lines above, but in the opposite direction. Now, by controlling the distance of each to their anchor, we have zero net force on the body but each line has a "pretension". with large pretension in mooring line stiffness increases. The greater the pretension, the stiffer the system becomes. We cannot have such a large pretension that for a small movement, or the line breaks.
the higher the pretension, the less the body will move, but the tendency to break a line is also greater.
excitation forces as described above can be categories in three terms.
Static forces can be calculated by applying the force on the body and finding maximum excursion due to external forces. In this scenario, there will be a equilibrium in external forces and mooring line tension. Include the stiffness of the mooring system in the frequency domain equations of motions and the total excursion will be the sum of the static and frequency domain motions. Knowing the position, we can back calculate the tensions. But stiffness in mooring line is non linear term and any approximation will have to dealt with non linearity. In this calculation stiffness is assumed at mean position of mooring line.
So we have two component of wave load. 1st order harmonic load on mooring system and 2nd order drift force loads on mooring system.
For normal barge maximum 1st order sway force occurs around 10 to 15 second and second order drift load occurs at higher period approximately 100 seconds. So wave mooring loads becomes significant around 100 seconds as , harmonic load and drift load combines and gives worst effect loading. Tension and motion behaviour of mooring lines are quite magnified at these higher periods around 100 seconds.
In general, if we are serious about analyzing a mooring system, we need to perform an analysis which includes all three parts of the excitation. If, however, we have a very stiff system then it will not be susceptible to large period forcing and a simple frequency domain approach will suffice.
Capabilities of the mooring system shall be computed using quasi-dynamic simulations of the vessel and the mooring system under combination of wind, wave and current environmental loads. Simulations shall consider combining wave frequency and low frequency responses of the system to get the maximum vessel motions and mooring line tensions.
Simulations shall performed for 3 hours duration environments. “Quasi-dynamic analysis” is performed, meaning that full dynamic motion of the vessel is considered but line tensions are estimated from vessel dynamic motions with static restoring curves.
The low frequency motion shall be computed in time domain while the wave frequency motion shall be calculated in frequency domain. The global dynamic motion is the superposition of the low frequency motion and the wave frequency motion, the stiffness shall be computed for the sum of the WF and LF motion.
The tension in the mooring line shall be higher than horizontal component. For mooring chain laying on the ground, there will be a constant difference in line tension and horizontal component of restoring force. Once the mooring chain gets up from bottom, these two force becomes almost same.
If mooring line stiffness is small, small change in force will produce large changes in position. For this reason, if one wants to stay close to a given position, he makes lines work in pairs. Suppose that we have two of the lines above, but in the opposite direction. Now, by controlling the distance of each to their anchor, we have zero net force on the body but each line has a "pretension". with large pretension in mooring line stiffness increases. The greater the pretension, the stiffer the system becomes. We cannot have such a large pretension that for a small movement, or the line breaks.
the higher the pretension, the less the body will move, but the tendency to break a line is also greater.
excitation forces as described above can be categories in three terms.
- Static forces (current, wind, and a mean wave force),
- Direct wave forces (forces at the wave period), and
- Non wave period forces (wave drift and wind gusts)
Static forces can be calculated by applying the force on the body and finding maximum excursion due to external forces. In this scenario, there will be a equilibrium in external forces and mooring line tension. Include the stiffness of the mooring system in the frequency domain equations of motions and the total excursion will be the sum of the static and frequency domain motions. Knowing the position, we can back calculate the tensions. But stiffness in mooring line is non linear term and any approximation will have to dealt with non linearity. In this calculation stiffness is assumed at mean position of mooring line.
So we have two component of wave load. 1st order harmonic load on mooring system and 2nd order drift force loads on mooring system.
For normal barge maximum 1st order sway force occurs around 10 to 15 second and second order drift load occurs at higher period approximately 100 seconds. So wave mooring loads becomes significant around 100 seconds as , harmonic load and drift load combines and gives worst effect loading. Tension and motion behaviour of mooring lines are quite magnified at these higher periods around 100 seconds.
In general, if we are serious about analyzing a mooring system, we need to perform an analysis which includes all three parts of the excitation. If, however, we have a very stiff system then it will not be susceptible to large period forcing and a simple frequency domain approach will suffice.
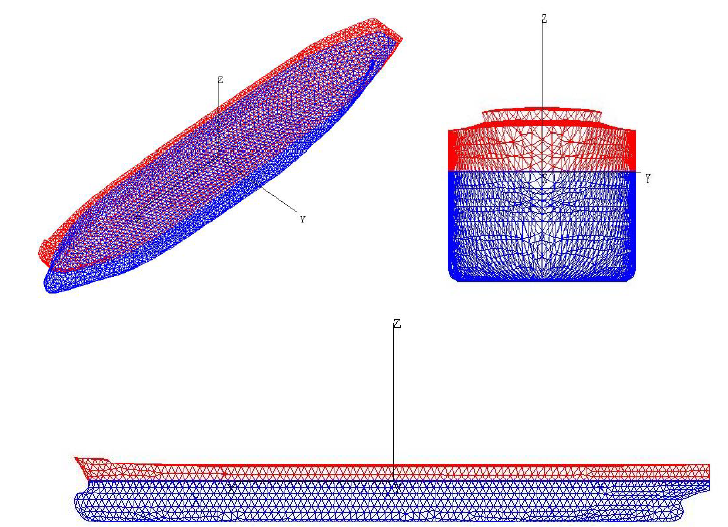
Hydrodynamic Analysis
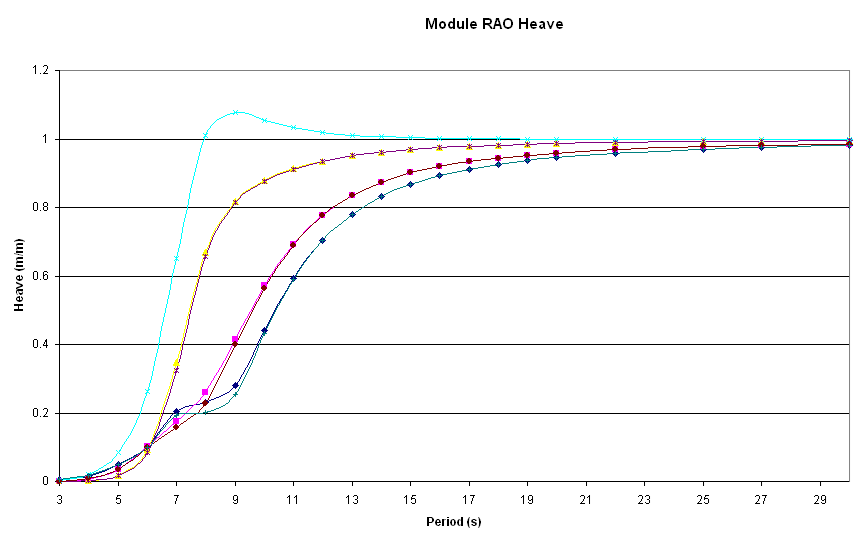
Diffraction radiation method evaluates hydrodynamic loads on a structure, submitted to regular waves and enables to get accurate RAOs operation of the vessel. Newman Approximation shall be considered for consideration of shallow water effects on drift loads.
RAO calculation for Barge Mooring analysis
Environmental Load Cases
The maximum allowable operational environmental conditions shall be estimated for each environmental direction assuming Wind and current are applied collinear to the wave direction and Directions are considered as coming from 0 to 337.5 deg and every equal intervals are screened.
Design Criteria
All mooring system criteria are majorly checked against the requirements of API RP 2SK, Design and Analysis of Station Keeping Systems for Floating Structures .
Mooring Line Design Strength
The tension in the mooring lines shall be checked against API RP 2SK requirements. The tension must therefore remain lower than:
- 50% of the MBL under intact condition
- 70% of the MBL under damage condition
Winch Brake Capacity
The maximum tensions in the mooring lines shall be lower than the winch brake capacity of mooring winches at first layer .
Anchor Holding Capacity
The maximum tension in the mooring line shall be lower than ultimate holding capacity of that particular type of anchor in specified ground conditions.
Anchor Uplift
No uplift at the anchor shall occur under intact condition. This criterion shall not be considered for damaged conditions (one line failure).Anchor uplift is checked against class requirements.Vertical load at the anchor should remain less than 20% of anchor’s wet weight.
Barge Clearance with Existing Facilities
The minimum horizontal clearance between barge and existing offshore structures shall shall be specified for intact and damage conditions.
Barge Excursion for mooring line clearance
For mooring line, a minimum horizontal clearance of 10m shall remain under intact condition and a minimum clearance of 3m with mooring line will be considered under damaged conditions.
Mooring line vertical Clearance with Subsea Facilities
Minimum vertical clearance of 15m shall be considered between mooring lines and existing pipelines for all the range of tension from allowable environments. If midline buoys are installed, the vertical force should not exceed 70% of the buoyancy capacity to ensure visibility.
Excursion after one Mooring Line damage
