MOORING BERTHING AND ANCHORAGE ENVIRONMENTAL LOADS ON TANKERS AND GAS CARRIERS (OCIMF-SIGTTO)
|
|
|
Introduction
The Master’s judgement and knowledge of the capability and limitations of anchoring systems, based on sound seamanship principles, is relied on when making decisions as to the potential security of an anchored vessel. However, unlike other mooring situations, such as mooring alongside using the ship’s outfit of lines, there is very little information available to assist in estimating the likely forces being imposed on the anchoring system. This calculator addresses this by providing a methodology and data to assist in estimating the forces acting on an anchored vessel in varying environmental conditions.
Scope
The forces acting on a ship when at anchor are primarily comprised of wind, current and wave drift loads. Wind loading data is presented for oil tankers and LNG carriers (prismatic and spherical containment systems) and is valid for vessels of 16,000 dwt and above.
Loads due to current are presented for oil tankers and are based on model test data for 190,000 dwt and above. The data is considered applicable for smaller vessel sizes down to 16,000 dwt.
Wave drift forces are presented for oil tankers from 20,000 dwt to 300,000 dwt and for LNG vessels of 150,000, 210,000 and 260,000 m3, irrespective of containment system type.
Key Assumptions
The process described in this paper is a simplified approach to estimating the forces acting on an anchored
vessel and is designed to be achievable through the application of relatively straightforward calculations. As a
result, a number of assumptions have been made which are briefly described, as follows:
current
waves (mean wave drift force).
Environmental Forces
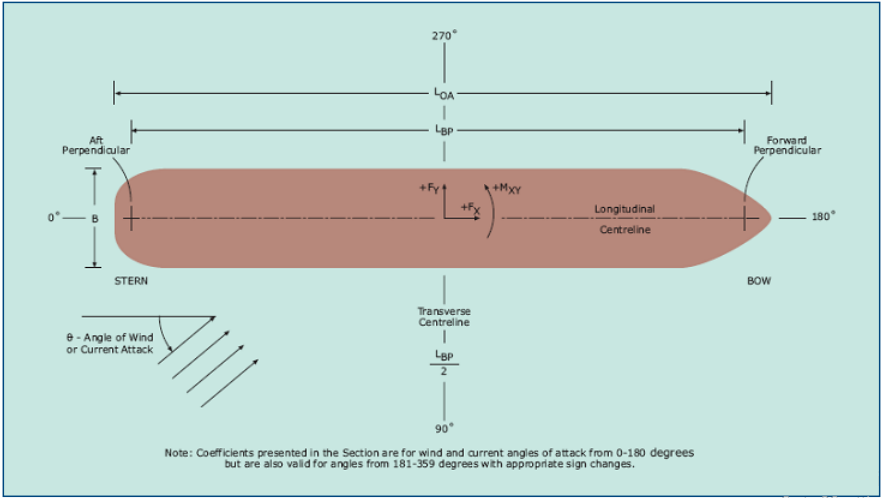
Calculations consider the environmental forces acting on an anchored vessel from wind, current and waves.
For wind and current loads, data is presented in the form of non-dimensional coefficient curves. For wave drift
forces, three dimensional surface plots are presented.
Note: where data is available for a specific ship, this should be used in preference to the general data presented here.
When comparing the OCIMF/SIGTTO drag data in this paper with that from other sources, it should be noted that the data has been increased above the original measured mean results to allow for scatter in the raw data, scaling effects and variations in hull geometry. This resulted in the wind drag coefficients for VLCCs being increased by 20% and those for LNG vessels by 10%.
No increase in the measured data has been made to the current drag coefficients. Wave drift forces have been taken from calculation of Tension Technology International (TTI) Ltd.
As it is assumed the vessel lies at a single anchor and will swing to an equilibrium position as a result of the combined action of wind, current and waves, it is considered necessary only to calculate the longitudinal force components when assessing the force acting on the anchored vessel.
Through the application of several equations, the magnitude of the total environmental force may be calculated. This value can then be compared to the anchor holding power to provide guidance as to whether the anchor is likely to drag.
Wind Loads
OCIMF has published wind load data in ‘Mooring Equipment Guidelines’ (MEG3) which includes a method of estimating the wind loads.
The wind force prediction is based on wind tunnel model tests using four models representing tankers of 155, 280, 400 and 500 kdwt, and involves the use of non-dimensional coefficients which were transferred into curves relating the wind angle to coefficient magnitude. Knowledge of the wind speed, direction and cross sectional area of the vessel allows a force to be estimated.
Recent model test data on more modern tanker forms confirms that the same coefficients are, in most cases, sufficiently accurate when applied to smaller ships and that they therefore may be used for a range of oil tankers down to approximately 16,000 dwt.
OCIMF/SIGTTO conducted wind tunnel tests to determine the wind load coefficients for LNG vessels in the 75,000 m3 - 125,000 m3 range. Zero trim was assumed in all cases and two cargo containment types were considered (spherical and prismatic-type tanks).
The coefficients are only valid for vessels with superstructures at the stern. The coefficient ‘CXw‘ and area ‘AT’ refer to the head-on projected area of the above waterline portion of the vessel.
Changes in freeboard have the most significant impact on the wind coefficient. Separate curves have therefore been developed for the fully loaded and ballasted conditions.
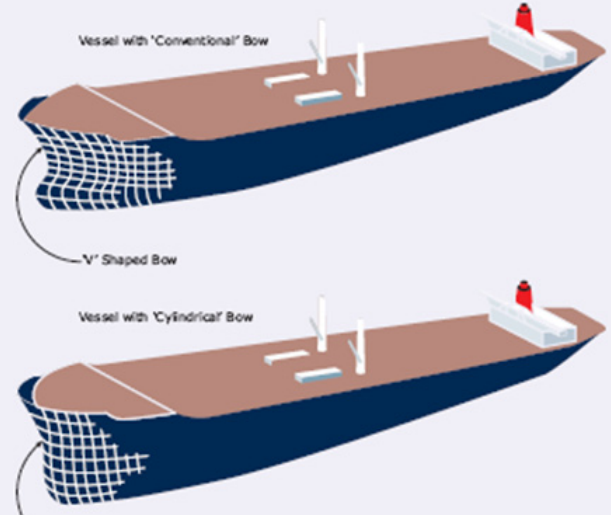
Variations in bow configuration also produce a substantial difference in the longitudinal force coefficient for a ballasted tanker. For consistency with MEG3, the configuration changes are characterised by tankers with a so-called ‘conventional’ bow shape, versus a ‘cylindrical’ bow shape.
The wind drag coefficients assume zero trim in the fully loaded condition and, for tankers, 0.8 degrees trim in the ballast condition.
The presence of spherical tanks on gas carriers has the most significant impact on the wind drag coefficient. The deviations in the coefficients result from the differences in the relative force contribution and distribution due to the configuration of the spherical tanks. Therefore, separate curves for prismatic and spherical tanks have been developed where the deviations are significant. Differences in wind loads due to the ship’s loaded condition are not significant due to the relatively small change in draught from a ballasted to fully loaded condition for the size of gas carriers reviewed.
Wind load calculation procedure
Step 1: Determine the ship characteristics
note the bow configuration
measure/estimate wind speed and heading relative to the stern
note the height of the wind speed measuring point above the surface of the water.
Step 2: Obtain the wind drag coefficients
Obtain the value CXw relating to the wind heading angle using Figure B1 for oil tankers and Figure B2 for LNG
vessels.
Step 3: Correct wind velocity for the measuring height
where:
VW = wind velocity at 10 m height (m/s)
vw = the wind velocity at elevation h (m/s)
h = elevation above ground/water surface (metres)
Step 4: Calculate longitudinal wind force component
Substitute CXw, ρw, VW, AT into the following equation:
Current Loads
It should be noted that unlike longitudinal wind drag calculated using transverse sectional area, the longitudinal current drag is calculated by reference to the hull length multiplied by the draught. Underkeel clearance has the greatest influence on the current drag coefficient. This is primarily due to the blockage effect of the hull that causes a proportionally larger volume of water to pass around rather than under the hull as the under keel clearance decreases.
The magnitude of the current forces is also influenced by the bow form in a similar manner to the wind. For a cylindrical bow with a bulb, it is recommended to use the data for the cylindrical bow without a bulb. For the conventional bow shape without bulb, the larger coefficient with or without bulb should be used.
The test programme mainly considered L/B ratios between 6.3 and 6.5 to reflect the majority of existing VLCCs at the time. However, more recent VLCCs tend to have L/B ratios in the range from 5.0 to 5.5. As L/B ratios decrease, the longitudinal drag coefficients tend to increase. For a VLCC with an L/B of 5.0, a maximum increase in the longitudinal drag coefficients of 25-30% may be expected for smaller current angles (up to a maximum of 15 degrees).
The trim is assumed to be zero for all the current drag data and the effects of trim on current coefficients have not been investigated.
Current load calculation procedure
Step 1: Determine the ship characteristics
LBP and draught (T)
note the bow configuration
measure/estimate current speed and heading relative to the stern
note the depth at which the current was measured and express as a percentage of the vessel’s draught.
Step 2: Obtain the longitudinal current drag force coefficient
CXc relating to the current heading angle using Figures B3 - B8 as appropriate, depending on water
depth:draught ratio (WD/T).
Step 3: Correct for average current
Obtain the current velocity correction factor, K from Figure B9 for the specific depth: draught ratio and for the
depth the current velocity is measured (as a % of ship draught).
Step 4: Compute the average current velocity
Step 5: Calculate longitudinal current force
Substitute CXc, ρc, VC, LBP, T into the following equation:
Wave Drift Forces
The mean force induced by waves is related to the reflection of the incident wave by the immersed body, and the movements/oscillations of the body (i.e. pitch and heave). Generally, waves of shorter period are reflected when they come into contact with the ship’s hull, which imparts a greater force than a longer wave, which tends to ‘roll’ past the vessel, exerting a lower drift force.
Wave drift force data is based on analysis performed by Tension Technology International Ltd. (TTI) for a range of ship types in varying sea states.
A Pierson-Moscowitz sea spectrum was used in the analysis, which represents a fully developed sea. All vessels were considered in the loaded condition.
Wave Height
Wave height is defined as the ‘significant wave height’ which is the average wave height (trough to crest) of the one-third largest waves. There is generally good agreement between the wave heights estimated by an observer and the actual significant wave height. Drift force increases with significant wave height and is proportional to wave height squared
Wave Period
The wave period used refers to the ‘Mean Wave Period’. Shorter wave periods generally result in higher drift forces; when the wave comes into contact with the ship’s hull, the wave is largely reflected
Depth: Draught Ratio
Analysis showed that the wave drift force is influenced by the ratio of water depth to ship draught (WD/T) and that for low WD/T ratios (for example, 1.2) the reduction in underkeel clearance at higher wave heights began to impact the analysis, leading to uncharacteristically high drift forces occurring. This occurrence was shown to reduce as the WD/T ratio increased, and no undue effects were recorded at WD/T = 2, which were in the same order of magnitude as higher WD/T ratios. Using WD/T = 2 was also felt to be appropriate when considering the IACS design criteria of a cable scope (the ratio of cable paid out to the water depth) of between 6 and 10.
Wave Heading
Head sea conditions result in only longitudinal wave drift forces acting on the vessel. However, as the wave heading shifts, transverse forces begin to dominate and the total drift force acting on the vessel increases markedly.
As an example, a VLCC in a 4m sea with a wave angle of incidence of 40 degrees to the bow would have a total resultant force acting on the hull of 74 tonnes, consisting of 35 tonnes of longitudinal force and 66 tonnes of transverse force. In such cases the vessel would swing at anchor as a result of the transverse force component until equilibrium is reached.
In certain cases, a vessel may yaw while at anchor. This may result in transverse forces being imposed on the vessel which may be transferred into the anchor chain cable. Generally, a 40 degree yaw angle can increase the total force acting on the chain by approximately a factor of 3.
It should be noted that the surface plots represent the longitudinal force acting on the vessel due to the specified wave conditions. For an anchored vessel which is in a steady state (i.e, lying at anchor and not Estimating The Environmental Loads On Anchoring Systems swinging) with the anchor chain deployed in line with the ship’s centreline, only the longitudinal components of forces are considered to be producing tension in the anchor chain.
However, it is recognised that the vessel may ‘yaw’ up to 40 degrees while at anchor, exposing the vessel’s side to the waves and resulting in both longitudinal and transverse forces being imposed on the ship. Transverse forces are markedly higher than the longitudinal forces for a given sea state, with the resultant total force that may be imposed on the anchor chain being of the order of 2-3 times higher than that presented in the surface plots.
In such conditions, the value obtained from the surface plot should be multiplied by 2 and 3, for 20 and 40 degrees yaw angles, respectively. Significant yawing will lead to high forces acting on the cable, although some may be damped by the
catenary in the chain cable.
Anchor Holding Power
Anchor holding power is influenced by the nature of the seabed and the fluke area. However, it is convenient to estimate the holding power of the anchor as a function of anchor weight. The following equation may be used to estimate the anchor holding power:
Anchor Holding Power (tonnes) = Anchor Weight (tonnes) x Seabed Factor
The Master’s judgement and knowledge of the capability and limitations of anchoring systems, based on sound seamanship principles, is relied on when making decisions as to the potential security of an anchored vessel. However, unlike other mooring situations, such as mooring alongside using the ship’s outfit of lines, there is very little information available to assist in estimating the likely forces being imposed on the anchoring system. This calculator addresses this by providing a methodology and data to assist in estimating the forces acting on an anchored vessel in varying environmental conditions.
Scope
The forces acting on a ship when at anchor are primarily comprised of wind, current and wave drift loads. Wind loading data is presented for oil tankers and LNG carriers (prismatic and spherical containment systems) and is valid for vessels of 16,000 dwt and above.
Loads due to current are presented for oil tankers and are based on model test data for 190,000 dwt and above. The data is considered applicable for smaller vessel sizes down to 16,000 dwt.
Wave drift forces are presented for oil tankers from 20,000 dwt to 300,000 dwt and for LNG vessels of 150,000, 210,000 and 260,000 m3, irrespective of containment system type.
Key Assumptions
The process described in this paper is a simplified approach to estimating the forces acting on an anchored
vessel and is designed to be achievable through the application of relatively straightforward calculations. As a
result, a number of assumptions have been made which are briefly described, as follows:
- The vessel is an oil tanker or an LNG carrier (spherical or prismatic) with accommodation aft
- Environmental forces acting on the vessel comprise:
current
waves (mean wave drift force).
- The data presented refers to the static condition. It should be noted that dynamic effects (e.g. yawing,pitching) can result in forces in the anchor system being 2 or 3 times higher than the estimated static forces.
- The environmental forces are considered as individual components that are summed to provide a total force. Interaction effects between the forces are not considered.
- The vessel is lying to a single anchor.
- The anchored vessel is in a steady position, having swung at anchor in the direction of the dominant environmental force or has reached an equilibrium position.
- The vessel lies at anchor such that the lead of the anchor chain is parallel to the centreline of the vessel. As a result, only the longitudinal components of the wind, waves and current forces need be considered.
- Wave drift forces have been estimated using a Pierson-Moskowitz sea spectrum.
- The catenary effect of the anchor chain is not considered
Environmental Forces
Calculations consider the environmental forces acting on an anchored vessel from wind, current and waves.
For wind and current loads, data is presented in the form of non-dimensional coefficient curves. For wave drift
forces, three dimensional surface plots are presented.
Note: where data is available for a specific ship, this should be used in preference to the general data presented here.
When comparing the OCIMF/SIGTTO drag data in this paper with that from other sources, it should be noted that the data has been increased above the original measured mean results to allow for scatter in the raw data, scaling effects and variations in hull geometry. This resulted in the wind drag coefficients for VLCCs being increased by 20% and those for LNG vessels by 10%.
No increase in the measured data has been made to the current drag coefficients. Wave drift forces have been taken from calculation of Tension Technology International (TTI) Ltd.
As it is assumed the vessel lies at a single anchor and will swing to an equilibrium position as a result of the combined action of wind, current and waves, it is considered necessary only to calculate the longitudinal force components when assessing the force acting on the anchored vessel.
Through the application of several equations, the magnitude of the total environmental force may be calculated. This value can then be compared to the anchor holding power to provide guidance as to whether the anchor is likely to drag.
Wind Loads
OCIMF has published wind load data in ‘Mooring Equipment Guidelines’ (MEG3) which includes a method of estimating the wind loads.
The wind force prediction is based on wind tunnel model tests using four models representing tankers of 155, 280, 400 and 500 kdwt, and involves the use of non-dimensional coefficients which were transferred into curves relating the wind angle to coefficient magnitude. Knowledge of the wind speed, direction and cross sectional area of the vessel allows a force to be estimated.
Recent model test data on more modern tanker forms confirms that the same coefficients are, in most cases, sufficiently accurate when applied to smaller ships and that they therefore may be used for a range of oil tankers down to approximately 16,000 dwt.
OCIMF/SIGTTO conducted wind tunnel tests to determine the wind load coefficients for LNG vessels in the 75,000 m3 - 125,000 m3 range. Zero trim was assumed in all cases and two cargo containment types were considered (spherical and prismatic-type tanks).
The coefficients are only valid for vessels with superstructures at the stern. The coefficient ‘CXw‘ and area ‘AT’ refer to the head-on projected area of the above waterline portion of the vessel.
Changes in freeboard have the most significant impact on the wind coefficient. Separate curves have therefore been developed for the fully loaded and ballasted conditions.
Variations in bow configuration also produce a substantial difference in the longitudinal force coefficient for a ballasted tanker. For consistency with MEG3, the configuration changes are characterised by tankers with a so-called ‘conventional’ bow shape, versus a ‘cylindrical’ bow shape.
The wind drag coefficients assume zero trim in the fully loaded condition and, for tankers, 0.8 degrees trim in the ballast condition.
The presence of spherical tanks on gas carriers has the most significant impact on the wind drag coefficient. The deviations in the coefficients result from the differences in the relative force contribution and distribution due to the configuration of the spherical tanks. Therefore, separate curves for prismatic and spherical tanks have been developed where the deviations are significant. Differences in wind loads due to the ship’s loaded condition are not significant due to the relatively small change in draught from a ballasted to fully loaded condition for the size of gas carriers reviewed.
Wind load calculation procedure
Step 1: Determine the ship characteristics
note the bow configuration
measure/estimate wind speed and heading relative to the stern
note the height of the wind speed measuring point above the surface of the water.
Step 2: Obtain the wind drag coefficients
Obtain the value CXw relating to the wind heading angle using Figure B1 for oil tankers and Figure B2 for LNG
vessels.
Step 3: Correct wind velocity for the measuring height
where:
VW = wind velocity at 10 m height (m/s)
vw = the wind velocity at elevation h (m/s)
h = elevation above ground/water surface (metres)
Step 4: Calculate longitudinal wind force component
Substitute CXw, ρw, VW, AT into the following equation:
Current Loads
It should be noted that unlike longitudinal wind drag calculated using transverse sectional area, the longitudinal current drag is calculated by reference to the hull length multiplied by the draught. Underkeel clearance has the greatest influence on the current drag coefficient. This is primarily due to the blockage effect of the hull that causes a proportionally larger volume of water to pass around rather than under the hull as the under keel clearance decreases.
The magnitude of the current forces is also influenced by the bow form in a similar manner to the wind. For a cylindrical bow with a bulb, it is recommended to use the data for the cylindrical bow without a bulb. For the conventional bow shape without bulb, the larger coefficient with or without bulb should be used.
The test programme mainly considered L/B ratios between 6.3 and 6.5 to reflect the majority of existing VLCCs at the time. However, more recent VLCCs tend to have L/B ratios in the range from 5.0 to 5.5. As L/B ratios decrease, the longitudinal drag coefficients tend to increase. For a VLCC with an L/B of 5.0, a maximum increase in the longitudinal drag coefficients of 25-30% may be expected for smaller current angles (up to a maximum of 15 degrees).
The trim is assumed to be zero for all the current drag data and the effects of trim on current coefficients have not been investigated.
Current load calculation procedure
Step 1: Determine the ship characteristics
LBP and draught (T)
note the bow configuration
measure/estimate current speed and heading relative to the stern
note the depth at which the current was measured and express as a percentage of the vessel’s draught.
Step 2: Obtain the longitudinal current drag force coefficient
CXc relating to the current heading angle using Figures B3 - B8 as appropriate, depending on water
depth:draught ratio (WD/T).
Step 3: Correct for average current
Obtain the current velocity correction factor, K from Figure B9 for the specific depth: draught ratio and for the
depth the current velocity is measured (as a % of ship draught).
Step 4: Compute the average current velocity
Step 5: Calculate longitudinal current force
Substitute CXc, ρc, VC, LBP, T into the following equation:
Wave Drift Forces
The mean force induced by waves is related to the reflection of the incident wave by the immersed body, and the movements/oscillations of the body (i.e. pitch and heave). Generally, waves of shorter period are reflected when they come into contact with the ship’s hull, which imparts a greater force than a longer wave, which tends to ‘roll’ past the vessel, exerting a lower drift force.
Wave drift force data is based on analysis performed by Tension Technology International Ltd. (TTI) for a range of ship types in varying sea states.
A Pierson-Moscowitz sea spectrum was used in the analysis, which represents a fully developed sea. All vessels were considered in the loaded condition.
Wave Height
Wave height is defined as the ‘significant wave height’ which is the average wave height (trough to crest) of the one-third largest waves. There is generally good agreement between the wave heights estimated by an observer and the actual significant wave height. Drift force increases with significant wave height and is proportional to wave height squared
Wave Period
The wave period used refers to the ‘Mean Wave Period’. Shorter wave periods generally result in higher drift forces; when the wave comes into contact with the ship’s hull, the wave is largely reflected
Depth: Draught Ratio
Analysis showed that the wave drift force is influenced by the ratio of water depth to ship draught (WD/T) and that for low WD/T ratios (for example, 1.2) the reduction in underkeel clearance at higher wave heights began to impact the analysis, leading to uncharacteristically high drift forces occurring. This occurrence was shown to reduce as the WD/T ratio increased, and no undue effects were recorded at WD/T = 2, which were in the same order of magnitude as higher WD/T ratios. Using WD/T = 2 was also felt to be appropriate when considering the IACS design criteria of a cable scope (the ratio of cable paid out to the water depth) of between 6 and 10.
Wave Heading
Head sea conditions result in only longitudinal wave drift forces acting on the vessel. However, as the wave heading shifts, transverse forces begin to dominate and the total drift force acting on the vessel increases markedly.
As an example, a VLCC in a 4m sea with a wave angle of incidence of 40 degrees to the bow would have a total resultant force acting on the hull of 74 tonnes, consisting of 35 tonnes of longitudinal force and 66 tonnes of transverse force. In such cases the vessel would swing at anchor as a result of the transverse force component until equilibrium is reached.
In certain cases, a vessel may yaw while at anchor. This may result in transverse forces being imposed on the vessel which may be transferred into the anchor chain cable. Generally, a 40 degree yaw angle can increase the total force acting on the chain by approximately a factor of 3.
It should be noted that the surface plots represent the longitudinal force acting on the vessel due to the specified wave conditions. For an anchored vessel which is in a steady state (i.e, lying at anchor and not Estimating The Environmental Loads On Anchoring Systems swinging) with the anchor chain deployed in line with the ship’s centreline, only the longitudinal components of forces are considered to be producing tension in the anchor chain.
However, it is recognised that the vessel may ‘yaw’ up to 40 degrees while at anchor, exposing the vessel’s side to the waves and resulting in both longitudinal and transverse forces being imposed on the ship. Transverse forces are markedly higher than the longitudinal forces for a given sea state, with the resultant total force that may be imposed on the anchor chain being of the order of 2-3 times higher than that presented in the surface plots.
In such conditions, the value obtained from the surface plot should be multiplied by 2 and 3, for 20 and 40 degrees yaw angles, respectively. Significant yawing will lead to high forces acting on the cable, although some may be damped by the
catenary in the chain cable.
Anchor Holding Power
Anchor holding power is influenced by the nature of the seabed and the fluke area. However, it is convenient to estimate the holding power of the anchor as a function of anchor weight. The following equation may be used to estimate the anchor holding power:
Anchor Holding Power (tonnes) = Anchor Weight (tonnes) x Seabed Factor